 Τα μαθηματικά και η μουσική είναι δυο επιστήμες που έχουν πολύ μεγάλη σχέση μεταξύ τους. Από την αρχαιότητα ακόμη οι δύο τέχνες αλληλεπιδρούν μεταξύ τους και η αλληλεπίδραση αυτή φτάνει ως τις μέρες μας...
Τα μαθηματικά και η μουσική είναι δυο επιστήμες που έχουν πολύ μεγάλη σχέση μεταξύ τους. Από την αρχαιότητα ακόμη οι δύο τέχνες αλληλεπιδρούν μεταξύ τους και η αλληλεπίδραση αυτή φτάνει ως τις μέρες μας...
Η ιδέα της σύνδεσης των μαθηματικών και της μουσικής γεννήθηκε πριν από 26 ολόκληρους αιώνες στην αρχαία Ελλάδα από τον Πυθαγόρα, μαθηματικό και ιδρυτή της πυθαγόρειας σχολής σκέψης. Ο φιλόσοφος γνώριζε πολύ καλά τη σχέση της μουσικής με τους αριθμούς. Οι ειδικοί ερευνητές θεωρούν ότι το πιθανότερο είναι πως ο ίδιος και οι μαθητές του εντρύφησαν στη σχέση της μουσικής και των αριθμών μελετώντας το αρχαίο όργανο μονόχορδο.
Όπως φαίνεται από το όνομά του, το μονόχορδο ήταν ένα όργανο με μία χορδή και ένα κινητό καβαλάρη που διαιρούσε τη χορδή επιτρέποντας μόνο ένα τμήμα της να ταλαντώνεται.που από αρκετούς μελετητές τοποθετείται στην οικογένεια του λαούτου δηλαδή με βραχίονα, χέρι. Το μονόχορδο χρησιμοποιήθηκε για τον καθορισμό των μαθηματικών σχέσεων των μουσικών ήχων. Ονομάζονταν και "Πυθαγόρειος κανών" γιατί απέδιδαν την εφεύρεσή του στον Πυθαγόρα. Πολλοί μεγάλοι μαθηματικοί εργάσθηκαν για τον υπολογισμό των μουσικών διαστημάτων πάνω στον κανόνα, όπως ο Αρχύτας (εργάσθηκε στις αναλογίες των διαστημάτων του τετραχόρδου στα τρία γένη, διατονικό, χρωματικό και εναρμόνιο και ανακάλυψε το λόγο της μεγάλης τρίτης στο εναρμόνιο γένος), ο Ερατοσθένης ο Δίδυμος (σ΄ αυτόν αποδίδεται ο καθορισμός του "κόμματος του Διδύμου", που είναι η διαφορά μεταξύ του μείζονος τόνου (9/8) και του ελάσσονος (10/9) δηλαδή 81/80).
Όμως, πώς ακριβώς πειραματίστηκαν οι Πυθαγόρειοι στο μονόχορδο,. για την ανάδειξη των σχέσεων μαθηματικών και μουσικής; Ήταν εντυπωσιακό το γεγονός ότι μόνο οι ακριβείς μαθηματικές σχέσεις έδιναν αρμονικούς ήχους στο μονόχορδο. Για παράδειγμα, έπρεπε να χωρίσουν ακριβώς στη μέση τη χορδή, και όχι περίπου στη μέση, ώστε να έχουν το ευχάριστο ψυχικό συναίσθημα που απορρέει από έναν αρμονικό ήχο
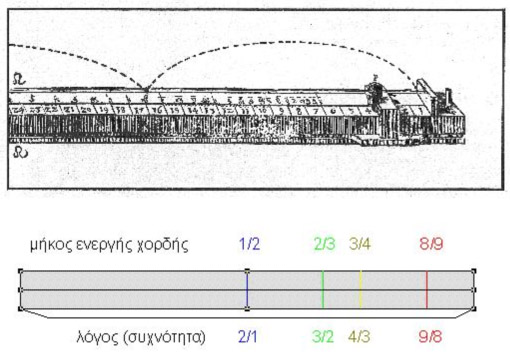
Αν μειώσουμε λοιπόν το μήκος μιας χορδής ακριβώς στο μισό, τότε ο ήχος που παράγεται είναι ακριβώς μία οκτάβα υψηλότερος (μία οκτάβα είναι ένα ντο, ρε, μι, φα, σολ, λα, σι, ντο) - μας δίνει, δηλαδή, ένα ντο πιο πάνω. Αν μειώσουμε το μήκος της χορδής κατά 1/3, τότε τα 2/3 της χορδής που απομένουν μας δίνουν τη διαφορά της πέμπτης (δηλαδή από το ντο στο λα). Κι αν μειώσουμε το μήκος κατά 1/4, τότε τα 3/4 που απομένουν μας δίνουν τη διαφορά της τετάρτης (από το ντο στο σολ). Ήταν ξεκάθαρο, λοιπόν, σ’ αυτό το επίπεδο της παρατήρησης ότι τα μαθηματικά "κυβερνούν" τη μουσική. Το γεγονός ότι από τους ήχους αυτών των διαφορών δημιουργείται ένα ευχάριστο συναίσθημα στον ακροατή, οδήγησε τους Πυθαγορείους στο συμπέρασμα ότι οι ακέραιοι και τα κλάσματα ελέγχουν όχι μόνο τον άψυχο αλλά και τον έμψυχο κόσμο μέσω της μουσικής
Για τους Πυθαγορείους, αυτή η άμεση και ακριβής σχέση μαθηματικών, μουσικής και ευχάριστου ψυχικού συναισθήματος αποτελούσε τη μέγιστη απόδειξη ότι η αλήθεια, στο ύψιστο επίπεδό της, εκφράζεται με μαθηματικές σχέσεις. Πίστευαν, μάλιστα, ότι η ψυχή, μέσα από τα μαθηματικά και τη μουσική, μπορούσε να εξυψωθεί ώσπου να ενωθεί με το σύμπαν και ότι ορισμένα μαθηματικά σύμβολα έχουν αποκρυφιστική σημασία. Στις αρχές της αρμονίας των Πυθαγορείων βασίστηκε η ευρωπαϊκή μουσική μέχρι, τουλάχιστον, τη στιγμή που ο Γιόχαν Σεμπάστιαν Μπαχ, μέσω της σύνθεσής του "Καλοσυγκερασμένο Κλειδοκύμβαλο" πρότεινε την υποδιαίρεση της οκτάβας σε δώδεκα ημιτόνια - κάτι, παρεμπιπτόντως, που είχε προτείνει δύο χιλιάδες χρόνια πριν από τον Μπαχ ο Αριστόξενος, όμως δεν εισακούστηκε
Συμπερασματικά, παρά τον ηθικοθρησκευτικό χαρακτήρα της διδασκαλίας του, ο Πυθαγόρας και οι μαθητές του διαμόρφωσαν φιλοσοφικές αρχές που επηρέασαν την πλατωνική και αριστοτελική διανόηση, κυρίως όμως συνέβαλαν στην ανάπτυξη των μαθηματικών, της μουσικής και της δυτικής φιλοσοφίας. Καθιέρωσαν την αντίληψη ότι η πραγματικότητα - συμπεριλαμβανομένης της μουσικής και της αστρονομίας- είναι στο βαθύτερο επίπεδό της μαθηματικής φύσης .
Οι Πυθαγόρειοι θεωρούσαν τον αριθμό 10 τέλειο. Επειδή αυτός προκύπτει από το άθροισμα των τεσσάρων πρώτων αριθμών 1+2+3+4=10, του έδωσαν το όνομα «τετρακτύς». Κατά τον Θέωνα το Σμυρναίο υπάρχουν έντεκα τετρακτύες που η κάθε μια εκφράζει ένα τομέα της φιλοσοφικής σκέψης στην αρχαιότητα. Ενδεικτικά αναφέρω ότι η 4η τετρακτύς δηλώνει τα τέσσερα απλά στοιχεία φωτιά, αέρα, νερό και γη, η 6η αναφέρεται στα γεωμετρικά σχήματα: με 1 εκφράζεται το σημείο, με 2 το μήκος, με 3 η επιφάνεια και με 4 το στερεό, η 8η δίνει τα συστατικά του ζώου: τα 1,2,3 αντιστοιχούν με το λογιστικό, το θυμικό και το επιθυμητικό, δηλαδή εκφράζουν την ψυχή, ενώ το 4 το σώμα.
Η μουσική κλίμακα του Πυθαγόρα κατασκευάζεται με βάση τις αναλογίες του κύβου, ο οποίος εκφράζεται με τον αριθμό 4 της 5ης τετρακτύος (1 = τετράεδρο, 2 = οκτάεδρο, 3 = εικοσάεδρο, 4 = κύβος) και συμβολίζει τη γη και το συνδυασμό των στοιχείων της. Ο κύβος έχει 6 έδρες, 8 κορυφές και 12 ακμές. Οι αριθμοί 12 και 6 δίνουν την αναλογία 2/1, οι 8 και 6 την αναλογία 4/3 ενώ οι 12 και 8 την αναλογία 3/2. Επίσης ο αριθμός 8 είναι το αρμονικό μέσο των 6 και 12, ενώ το αριθμητικό μέσο των αριθμών αυτών είναι ο 9. Ο αρμονικός και αριθμητικός μέσος δίνουν την αναλογία 9/8. Έτσι προκύπτουν οι μαθηματικές αναλογίες βάση των οποίων κατασκευάζεται η μουσική κλίμακα κατά τους Πυθαγόρειους. Οι αναλογίες αυτές αποδείχθηκαν και στην πράξη από τα πειράματα που έκανε ο Πυθαγόρας πάνω στο μονόχορδο το οποίο διαίρεσε σε 12 ίσα τμήματα (όσες και οι ακμές του κύβου).
Με τη χορδή «ανοιχτή» δηλαδή σε θέση να μπορεί να ταλαντώνεται όλο το μήκος της (λόγος 1, συχνότητα 1), έκρουσε και άκουσε ένα μουσικό τόνο. Στη συνέχεια περιόρισε το μέρος της χορδής που ταλαντώνεται στο μισό της μήκος, και βρήκε ότι ο ήχος που ακούστηκε είναι η διαπασών, αυτό που σήμερα ονομάζουμε οκτάβα. Το ύψος λοιπόν του ήχου επηρεάζεται από το μήκος της χορδής και μάλιστα όταν η αναλογία του μήκους είναι 1/2 (συχνότητα 2/1) έχουμε το διάστημα της οκτάβας. Έτσι ορίστηκαν τα άκρα της μουσικής κλίμακας, η υπάτη και η νήτη. Στη συνέχεια μετακινώντας τον καβαλάρη σε διάφορα σημεία, βρήκε ότι αν ταλαντωνόταν τα 3/4 της χορδής (συχνότητα 4/3) προέκυπτε ο τέταρτος φθόγγος από τους οκτώ μιας μουσικής κλίμακας, η μέση, ενώ αν ταλαντωνόταν τα 2/3 της χορδής (συχνότητα 3/2) προέκυπτε ο πέμπτος φθόγγος, η παραμέση. Οι υπόλοιποι φθόγγοι της κλίμακας κατασκευάζονται χρησιμοποιώντας το λόγο 9/8 ως εξής:
- Ο δεύτερος φθόγγος προκύπτει από τον λόγο του πρώτου (υπάτη) αν τον πολλαπλασιάσουμε με 9/8: 1 x 9/8 = 9/8 δηλαδή για την παραγωγή του θα ταλαντώνονται τα 8/9 της χορδής.
- Ο τρίτος φθόγγος προκύπτει από τον λόγο του δεύτερου (9/8) αν και πάλι πολλαπλασιαστεί με 9/8: 9/8 x 9/8 = 81/64 δηλαδή θα ταλαντώνονται τα 64/81 της χορδής.
- Ο έκτος φθόγγος προκύπτει από τον λόγο του πέμπτου (παραμέση) που πολλαπλασιάζεται με 9/8: 1:2/3 x 9/8 = 27/16 δηλαδή θα ταλαντώνονται τα 16/27 της χορδής.
- Τέλος, ο έβδομος φθόγγος προκύπτει από τον λόγο του έκτου και πάλι πολλαπλασιαζόμενου με 9/8: 1:16/27 x 9/8 = 243/128 δηλαδή για την παραγωγή του θα ταλαντώνονται τα 128/243 της χορδής.

Πέρα από το μονόχορδο, ο Πυθαγόρας πειραματίστηκε και με άλλα υλικά και τις ιδιότητές τους που συνθέτουν τα μουσικά διαστήματα, όπως η τάση χορδών ίσου μήκους και πάχους, το μήκος ηχητικού σωλήνα κ.τ.λ. Ο χωρισμός και καθορισμός των μουσικών διαστημάτων που πέτυχε, ήταν ένα τεράστιας σημασίας επίτευγμα τόσο για τη μουσική και τη θεωρία της όσο και για τα μαθηματικά και τη δύναμή τους να ερμηνεύουν τον κόσμο με αριθμούς όπως εξάλλου δίδασκε και ο Πυθαγόρας. Πέρα από τη μεγάλη σημασία για τη θεωρία της μουσικής, ο υπολογισμός του έδωσε την ευκαιρία να κατασκευαστούν μουσικά όργανα με μεγαλύτερη ακρίβεια από πριν.
Με το πέρασμα του χρόνου, η Πυθαγόρεια μουσική κλίμακα τροποποιήθηκε είτε για πρακτικούς είτε για καθαρά φιλοσοφικούς λόγους, όμως ο Πυθαγόρας είχε δείξει έναν δρόμο που και οι σύγχρονες μουσικές κλίμακες ακολουθούν. Ακόμα και σήμερα υπολογίζουμε μαθηματικά τα μουσικά διαστήματα τα οποία βέβαια έχουν διαφοροποιηθεί σημαντικά από τότε.
Ο Αριστόξενος, νεότερος του Πυθαγόρα (περί το 375 π.Χ.) υπήρξε φιλόσοφος και σημαντικότατος θεωρητικός της μουσικής και του δόθηκε μάλιστα η ονομασία «ο Μουσικός». Η μέθοδός του ήταν κυρίως εμπειρική. Το σύστημα διδασκαλίας του βασίζεται σε αντίθεση με τον Πυθαγόρα, στην ικανότητα του αυτιού να αντιλαμβάνεται την αρμονική σχέση των μουσικών τόνων. Δεν ερευνά τις αριθμητικές σχέσεις μέσα στην οκτάβα, όμως καθορίζει τον ολόκληρο και τον μισό τόνο και κατασκευάζει μια κλίμακα με βάση το ένα δωδέκατο του τόνου.
Ο Ευκλείδης από την άλλη, έχει μια γεωμετρική πρόταση για τα μουσικά διαστήματα. Θεωρεί ότι αντιστοιχούν σε ευθείες γραμμές, με μία όμως διαφορά: ενώ οι ευθείες γραμμές που παράγονται ως αριθμοί, ορίζονται με δύο γράμματα ένα στην αρχή και ένα στο τέλος τους, τα μουσικά διαστήματα δηλώνονται με ένα γράμμα.

Στη σημερινή πραγματικότητα, τόσο η μουσική θεωρία, όσο και η μουσική πράξη, ερμηνεύονται με φυσικούς νόμους, που με τη σειρά τους διατυπώνονται με μαθηματικές σχέσεις.
Στην ακουστική (στον ιδιαίτερο κλάδο της φυσικής που έχει ως αντικείμενο τον ήχο και τις ιδιότητές του) ένα μουσικό διάστημα εκφράζεται σαν ο λόγος δύο συχνοτήτων. Σε ορισμένες περιπτώσεις ο λόγος είναι απλής μορφής όπως για παράδειγμα οι γνωστοί μας λόγοι της καθαρής πέμπτης (3/2), της καθαρής τετάρτης (4/3), της οκτάβας (2/1) κ.λ.π. Σε άλλες περιπτώσεις, ελλείψει μεγίστου κοινού διαιρέτη, οι όροι του λόγου είναι μεγάλοι αριθμοί όπως στο διάσχισμα (2048/2025). Προκύπτει λοιπόν το συμπέρασμα ότι είναι δύσκολη, αν όχι αδύνατη, η σύγκριση δύο μουσικών διαστημάτων.
Η απλούστευση στην παράσταση των μουσικών διαστημάτων επήλθε με τη βοήθεια της λογαριθμικής σχέσης
μέγεθος μουσικού διαστήματος = k * log(f2/f1)/log2
στην παραπάνω σχέση, όπου f1, f2 οι συχνότητες των φθόγγων του μουσικού διαστήματος και f2>f1. Το k είναι μια σταθερά η τιμή της οποίας καθορίζει και ένα σύστημα μονάδων μουσικών διαστημάτων.
Συγκερασμοί για τα μουσικά διαστήματα
Ανάλογα με τις τιμές της σταθεράς k (οι οποίες αφορούν διαίρεση της οκτάβας σε τόσα τμήματα όσο η αντίστοιχη τιμή), έχουμε κι ένα σύστημα μονάδων μουσικών διαστημάτων. Οι πιο γνωστές και χαρακτηριστικές τιμές της σταθεράς k, αναφέρονται στη συνέχεια.
ΤΙΜΗ ΣΤΑΘΕΡΑΣ k ΟΝΟΜΑΣΙΑ ΜΟΝΑΔΑΣ ΤΩΝ ΜΟΥΣΙΚΩΝ ΔΙΑΣΤΗΜΑΤΩΝ
12 .................Συγκερασμένο Ευρωπαϊκό ημιτόνιο
53 .................κόμμα του Μερκάτορα
68 .................Αραβική μονάδα, βυζαντινό ηχομόριο
72 .................Βυζαντινό ηχομόριο
301 ...............Savart
665 ...............Delfi unit
1200 ..............cent
ΠΗΓΕΣ
Ελληνική ιστοσελίδα για τη Βυζαντινή μουσική , Focus , Πανελλήνιο Σχολικό δίκτυο
-
 Κώστας Μπίγαλης: Η φιλοσοφία της ζωής μου είναι το «εμείς» και όχι το «εγώ»
Κώστας Μπίγαλης: Η φιλοσοφία της ζωής μου είναι το «εμείς» και όχι το «εγώ»
-
 Martha
Martha
-
 Άννα Μπιθικώτση: Για µένα κάθε λέξη, κάθε εικόνα είναι βιωμένη
Άννα Μπιθικώτση: Για µένα κάθε λέξη, κάθε εικόνα είναι βιωμένη
-
 10 Τραγούδια που Προέβλεψαν το Μέλλον
10 Τραγούδια που Προέβλεψαν το Μέλλον
-
 Δημιουργώντας ένα Υποθετικό Album των Beatles στη Δεκαετία του '70
Δημιουργώντας ένα Υποθετικό Album των Beatles στη Δεκαετία του '70
-
 Δίσκος piezo κιθάρας στα επιστόμια γλωττιδόφωνων
Δίσκος piezo κιθάρας στα επιστόμια γλωττιδόφωνων
- Αρχείο
Aρθρα
Γίνε ΣΥΝΤΑΚΤΗΣ
Αν σου αρέσει να γράφεις για μουσικά θέματα, σε περιμένουμε στην ομάδα συντακτών του ιστορικού, ανεξάρτητου, πολυφωνικού, υγιούς και δημοφιλούς ηλεκτρονικού περιοδικού μας.
Στείλε το άρθρο σου
σχολιάστε το άρθρο
Για να στείλετε σχόλιο πρέπει να είστε μέλος του MusicHeaven. Παρακαλούμε εγγραφείτε ή συνδεθείτε
| #749 / 26.08.2004, 03:44 / Αναφορά Χαιρομαι πραγματικά orpfeus για το συγκεγριμένο άρθρο σχετικά με τη θεωρία και ιστορία της μουσικής ! Ειναι απο τα καλύτερα που έχω διαβάσει μέσα σε αυτό το σαίτ....και εύχομαι να συνεχιστεί!!! Εκτιμώ βαθιά ! την διάθεσή σου να μπεις σε αυτή την τόσο χρήσιμη ανάλυση και να ξεδιπλώσεις αυτήν την διάσταση σχέσης μαθηματικών-μουσικής απο τον Πυθαγόρα. Προσωπικά , πιστευοντας στη συμπαντική σχέση της μουσικής με τον άνθρωπο και στη Πυθαγόρεια φιλοσοφία, εκτιμώ οτι η κωδικοποίηση δια μέσου των αριθμών (κατ'επέκταση και στη μουσική)εμπεριέχει την σοφία του γίγνεσθε και τις σταθερές, που δίνουν απαντήσεις. Βέβαια η κλίμακα ειναι ένα όριο, κωδικοποιημένο, που μας βοηθά να ερμηνευουμε , να εκπαιδευουμε τις βαθύτερες προεκτάσεις της εωτερικότητάς μας, άλλά ,παραμένει μία λόγική ερμηνεία. Δεν ξέρω αν αυτό αποτελεί την ΑΛΗΘΕΙΑ? ( μιλώ για αλήθεια , εχοντας ως δεδομένο οτι η αλήθεια της γνώσης ειναι περιορισμένη) Το εκπληκτικο για μένα ειναι , οτι μια λογική κατάσταση μπορει να κινητοποιεί το συγκινησιακό μας πεδίο......( που κατά την αποψή μου δεν εμπεριέχει λογικές διεργασίες) ισως βέβαια αυτό, να αποτελεί ένα άλλο μεγάλο κεφάλαιο συζήτησης (λογική+μουσική)....... Ωστόσο θέλω να πώ οτι το διάστημα της οκτάβας, παρότι θεωρητικά μπορούμε να το υποδιαιρέσουμε σε άπειρα τμήματα, το αυτί μας αντιλαμβάνεται μόνον εκείνες τις αποστάσεις που ειναι μεγαλύτερες απο το 1/100 και σε κάποιες ευνοϊκές περιοχές του ήχου το 1/180 της οκτάβας. Γιατί άραγε? Γιατί άραγε ? π.χ. ένα τζιτζίκι ακούει τρεις οκτάβες οξύτερους ήχους, απο εκείνες που συλλαμβάνει ο άνθρωπος? Ας πούμε, σε ποιά μαθηματική(λογική) σκέψη ή σχέση θα μπορούσαμε να έχουμε απαντήσεις σε αυτό? |
| #753 / 26.08.2004, 15:20 Τα μαθηματικά θέτουν και ερμηνεύουν. Η διαδρομή μας απέναντί τους πιστεύω οτι κρατά το μεγαλύτερο και το πιο ενδιαφέρον σημείο ακόμα κρυφό. Η αλήθεια , όπως την αντιλαμβανόμαστε εμεις , είναι και αυτή διαστασιολογημένη. Η σύλληψή της ακόμα σε πρώιμο στάδιο. Η μαθηματική(λογική) σχέση ή σκέψη μέσω τις οποίας θα μπορούσαμε να δώσουμε απαντήσεις σε διάφορα φαινόμενα είναι μια Ιθάκη με όλες τις ενδιάμεσες παραμέτρους και την υπέροχη διαδρομή με τις ανακαλύψεις της. Η λογική και η μουσική όπως αναφέρεις έχουν σχέση , όπως πιστεύω και με το συγκινησιακό μας πεδίο. Επαγωγικά λοιπόν θα μπορούσαμε να χαρακτηρίσουμε τα συναισθήματα αρρηκτα δεμένα με μαθηματικες "αλήθειες" αλλα αυτο όντως χρειάζεται μεγάλη συζήτηση. |
| #754 / 26.08.2004, 16:51 / Αναφορά Πολύ ενδιαφέρον το άρθρο σου Γιώργο. Φαντάζει αρχικά πεζό κι όμως είναι έτσι, η μουσική είναι μαθηματικές σχέσεις κι αριθμοί. Ο Πυθαγόρας ήταν ο πρώτος όπως αναφέρεις ο οποίος μελέτησε τους ήχους και διατύπωσε κάποιους μαθηματικούς τύπους, για να διευκολύνει την παραπέρα μελέτη τους. Ακόμη και σήμερα, η μουσική ανάλυση βασίζεται στους τύπους του Πυθαγόρα. Πέραν όμως της μουσικής, οι Πυθαγόρειοι φιλόσοφοι θεοποίησαν την αριθμολογία, προσπαθώντας να ερμηνεύσουν με μαθηματικά όλες τις πτυχές της ζωής, όπου δεν χωράν πάντα οι αριθμοί και έτσι κατέληξαν στη στρέβλωση και τον αποκρυφισμό. |
| #755 / 26.08.2004, 17:47 Πράγματι πολύ καλό άρθρο. Επί του θέματος μήπως υπάρχουν κάπου ηχογραφήσεις αρχαίας ελληνικής μουσικής και αν ναι που; Παλιά διάβασα ότι διάφοροι δοκίμασαν να αναπαραστήσουν την αρχαία ελληνική μουσική (ανα)κατασκευάζοντας και τα απαραίτητα όργανα αλλά δεν θυμάμαι περισσότερες λεπτομέρειες. Οσο για την θεοποίηση των Μαθηματικών, πιστεύω ότι όσο περνούν τα χρόνια η ανθρωπότητα θα ανακαλύπτει ότι τα Μαθηματικά κρύβονται πίσω από πολλές πτυχές της ύπαρξης και του κόσμου γενικότερα. Η αρχή έχει γίνει με την κβαντική φυσική... ΥΓ Με τις σημερινές θρησκείες να φθίνουν,κάτι πρέπει να βρεθεί για να αναπληρώσει το κενό..food for thought :) |
| #757 / 27.08.2004, 09:19 Απόπειρες ηχογράφησης αρχαίας Ελληνικής μουσικής έχουν γίνει αρκετές. Από τις πιο αξιόπιστες είναι αυτή του Χριστόδουλου Χάλαρη, με την ορχήστρα Λεπτών οργάνων, που απαρτίζεται από όργανα που κατασκευάστηκαν βάσει ιστορικών στοιχείων, έτσι ώστε η όψη και ο ήχος τους, να προσεγγίζει όσο το δυνατόν περισσότερο, αυτή των αρχαίων μουσικών οργάνων. Κάτι που δεν γνωρίζουν πολλοί, είναι ότι παρτιτούρες με αρχαία Ελληνική μουσική έχουν διασωθεί πολλές, δυστυχώς όμως, δεν ασχολείται σχεδόν κανείς μ' αυτές. Σίγουρα τα μαθηματικά μπορούν να ερμηνεύσουν πολλά μυστήρια του κόσμου. Όπως λες κι εσύ ένα από τα σύγχρονα επιστημονικά προβλήματα είναι π.χ. η κβάντωση όλων των ενεργειακών πεδίων, που επιχειρούν να τεκμηριώσουν, χρησιμοποιώντας το μαθηματικό μοντέλο των Υπερχορδών. Όμως, όταν τα μαθηματικά χρησιμοποιούνται και για την ερμηνεία μεταφυσικών θεμάτων, όπως η σύσταση και η δομή της ψυχής, του πνεύματος κλπ. είναι....μαθηματικά αποδεδειγμένο ότι καταλήγουν στη δημιουργία επικίνδυνων αποκρυφιστικών αιρέσεων και σεκτών. Όσον αφορά το θέμα των θρησκειών που θίγεις, εδώ χωράει πολύ συζήτηση και θα βγούμε εκτός θέματος. Έναν προβληματισμό καταθέτω μόνο. Τελικά, οι θρησκείες φθίνουν, ή ο σύγχρονος άνθρωπος, που θεοποιώντας τον ευδαιμονισμό, δεν έχει αφήσει στην καρδιά του χώρο για τίποτε άλλο; |
| #2179 / 12.05.2005, 11:21 / Αναφορά Θα ήθελα να σταθώ σε 2 σημεία του άρθρου... α. Πού ακριβώς αναφέρεται ότι ο Αριστόξενος είχε προσπαθήσει να εισηγάγει την συγκερασμένη κλίμακα (πολύ πριν από τον Μπαχ) όπως αναφέρεις; Θα προτιμούσα ακριβή πηγή αρχαίου κειμένου εάν είναι δυνατόν, γιατί γνωρίζω κάποια πράγματα για την Αρχαία Ελληνική Μουσική και αυτό δεν το έχω ακούσει πουθενά. β. Αναφέρεις πιο πάνω ότι "σε αυτό το σημείο τα μαθηματικά κυβερνούν την μουσική". Θα 'λεγα πως είναι λίγο άστοχος ο χαρακτηρισμός σου, γιατί με την ίδια λογική τα μαθηματικά κυβερνούν όλες τις τέχνες, κυβερνούν το ανθρώπινο σώμα, κυβερνούν την φύση και κυβερνούν όλο το σύμπαν. Αν συμβαίνει κάτι τέτοιο τότε θα πρέπει να είμαστε πολύ ανόητοι για να μην έχουμε ανακαλύψει ακόμη (μετά από 2000+ χρόνια) ποια μαθηματικά κυβερνούν την μουσική και να υπάρχουν άνθρωποι που να δηλώνουν συνθέτες και να πληρώνονται γι' αυτό. Τέλος πάντων, αυτό που θέλω να πω, γιατί φαντάζομαι ήδη την αντίδρασή σου (εγώ μίλησα γι' αυτό το συγκεκριμένο σημείο και όχι γενικοτερα...κλπ...κλπ...), αν υποθέσουμε ότι τα μαθηματικά είναι το αβγό, και η μουσική η κότα, τελικά η κότα έκανε το αβγό ή το αβγό την κότα. Θέλω να πιστεύω πως ΝΑΙ είναι σε ένα μεγάλο βαθμό αλληλένδετα, αλλά πρέπει να λαμβάνουμε πάντοτε υπόψην μας την εποχή, τις κοινωνικοπολιτικές συνθήκες, το ότι ο άνθρωπος είναι ζώο μιμητικό (κάνει μουσική μέσα από τις όποιες εμπειρίες του), και προπάντων ότι υπάρχει και κάτι περισσότερο από το αβγό και την κότα που σε μία γενική αποδοχή φέρει το όνομα "Θεός". Τα μαθηματικά κατ' εμέ δεν προϋπάρχουν της μουσικής ή κατ' επέκτασιν τους σύμπαντος, είναι απλά the human way να κατανοήσουμε κάποια πράγματα. Και όπως και ο άνθρωπος έχουν και αυτά τα ανθρώπινα όριά τους. Η μουσική παίζει με άλλα όρια. |
| #2191 / 13.05.2005, 00:05 Για τον Αριστόξενο και την κλίμακα με βάση το ένα δωδέκατο του τόνου (και όχι τη συγκερασμένη - δεν την αναφέρει, άλλωστε, πουθενά σε σχέση με τον Αριστόξενο, ο Γιώργος στο άρθρο του): Macran, Henry S. 1902, The harmonics of Aristoxenos, Oxford: The Clarendon Press (reprint Georg Olms Verlag, Hildesheim, 1974, 1990) :-) |
| #2194 / 13.05.2005, 10:41 Καλή σου μέρα Lavic27. Kαταρχάς δε φαντάζεσαι την αντίδραση μου διότι είμαι απρόβλεπτος .... :). Kατα δεύτερον, ο Θεός είναι προσωπικός κατ ' εμέ όσον αφορά την ονοματολογία του και την αντίληψη καθενός για αυτόν. Δηλαδή για άλλους είναι ο Βούδας για άλλους ο Χριστός για άλλους η φύση για άλλους τα μαθηματικά. Δεν είναι αναγκαία κακό κάτι τέτοιο. Ο καθένας κάνει τις επιλογές του και ίσως κάποια στιγμή επαληθευτεί ή καταρριφθεί. Δεν είναι δόκιμο πιστεύω να ασχολούμαστε με το αν το αυγό έκανε την κότα ή το αντίθετο, ή τουλάχιστον να σπαταλάμε τόσο χρόνο σε κάτι που ακόμα δεν έχει ανακαλυφθεί επιστημονικά. Ίσως ο κόκκορας να μπορεί να μας δώσει μια πιο έγκυρη τοποθέτηση επι του θέματος. Όπως και να έχει πάντως, μας αρέσει ή όχι, ταυτιζόμενο ή μη με τις αντιλήψεις μας, τα πάντα στο γνωστό μέχρι τώρα σύμπαν υπόκεινται σε μαθηματικους όρους. Και εννοώ τα πραγματικά μαθηματικά και όχι τους τύπους που ανακάλυψαν κάποιοι σε αυτόν το κόσμο. Και αυτό δεν το βλέπω ούτε αρνητικά ούτε θετικά. Το βλέπω απλώς σα μια πραγματικότητα. |
| #2199 / 14.05.2005, 10:17 Δεν είπα ότι τα μαθηματικά δεν συνδέονται με τα πάντα. Είναι κάτι που το αποδέχομαι εως ένα πολύ μεγάλο βαθμό. Ωστόσο, αυτό που θέλησα να γίνει εμφανές στο σχόλιό μου ήταν το ότι ίσως θα έπρεπε να είμαστε σχετικά συγκρατημένοι απέναντι σε μια τέτοια αντίληψη, καθώς τα μαθηματικά που γνωρίζουμε είναι περιορισμένα. Μπορεί ο ανθρώπινος εγκέφαλος να είναι ο τελειότερος επεξεργαστής που υφίσταται σήμερα, και ο άνθρωπος το τέλειο PC καθώς εκμεταλλεύεται την φύση για να τροφοδοτείται, συν του ότι αναπαράγεται, όμως δεν είμαστε ακόμη ικανοί να κατανοήσουμε και κατά συνέπεια να θέσουμε μαθηματικούς κανόνες στην μουσική και κατ' επέκταση στην φύση και σίγουρα δεν θα γίνουμε ποτέ βλέποντας τηλεόραση (άσχετο, αλλά έτσι μου βγήκε). Πάντως όποιος ενδιαφέρεται περισσότερο για την Αρχαία Ελληνική Μουσική, παραπέμπω στο βιβλίο του M.L. West, Αρχαία Ελληνική Μουσική, κυκλοφορεί μεταφρασμένο και στα ελληνικά εδώ και 4-5 χρόνια, ο οποίος απ' όσο γνωρίζω είναι και ο εγκυρότερος μελετητής της Αρχαίας Ελληνικής Μουσικής μαζί με τον Barker. Τώρα γιατί οι ¶γγλοι ασχολούνται περισσότερο με την αρχαία μουσική μας απ' ότι εμείς...αυτό είναι ίσως ένα άλλο topic. |
| #6860 / 10.01.2007, 18:43 / Αναφορά Πραγματικά έχεις κάνει μια σπουδαία δουλειά. Αν και δεν είμαι ειδικός θεωρό πως το αποτέλεσμα της έρευνας σου σε δικαιώνει. Ωστόσο θα είχε ενδιαφέρον να συγκρίνεις την Πυθαγόρεια αντίληψη για τη σχέση μαθηματικών και μουσικής, με την άλλη μεγάλη σχολή της αρχαιότητας, αυτή του Αριστόξενου, για να καταλάβουμε πως υπήρχαν ακόμη και στην αρχαιότητα άνθρωποι που έβλεπαν πιο διασκεδαστικά την υπόθεση μουσική και όχι κατ’ ανάγκη ως επιστήμη. Αν σε ενδιαφέρει επικοινώνησε μαζί μου για να σε φέρω σε επαφή με έναν μαθηματικό μουσικολόγο, ο οποίος έχει θεμελιώσει την σχέση μεταξύ βυζαντινής και αρχαιοελληνικής μουσικής και οπωσδήποτε μπορεί να σε καθοδηγήσει καλύτερα από τον καθένα. |
| #11760 / 08.02.2008, 00:57 / Αναφορά Απλά εκπληκτικό! Ήξερα για τον Πυθαγόρα, αλλά αυτά που έμαθα είναι... |
| #12282 / 09.03.2008, 01:38 / Αναφορά Θα ακουστεί αρκετά σοβινιστικό, αλλά και πάλι οι Έλληνες έκαναν την αρχή και σ' αυτό...(Η αρχή είναι το ήμισυ του παντός!) |
| #13166 / 19.04.2008, 10:34 / Αναφορά Έχω τελειώσει μαθήματα ιστορίας μουσικής και δεν έχω μάθει τίποτα παρόμοιο... Πραγματικά εντυπωσιάστηκα... Ευχαριστώ βρε !!! |
| #14572 / 12.06.2008, 12:18 / Αναφορά Pragmatika uperoxo arthro! |
| #14699 / 17.06.2008, 12:32 / Αναφορά Εκ πρώτης είναι ένα συμπαθές άρθρο, αγαπητέ Ραψωδέ, απ’ την άλλη όμως το μέλος Laviq27 κάνει πολύ σωστές παρατηρήσεις που προβληματίζουν για την εγκυρότητά του. Είναι πράγματι τελείως αβάσιμη πληροφορία ότι ο Αριστόξενος ο Ταραντίνος είχε προτείνει τον συγκερασμό της κλίμακος όπως έκανε ο Μπαχ. Αυτό για μένα είναι παραπληροφόρηση. Επίσης πολύ εύστοχος ο προβληματισμός σου όσον αφορά τα μαθηματικά που κυβερνούν τη μουσική. Λες ο Μπετόβεν, ο Μότσαρτ, ο Λιστ να ήταν μαθηματικοί; Λες ο πατέρας μου που είναι μαθηματικός, να μπορεί να συνθέσει μουσική όπως ο Πέτρος ο Μπερεκέτης ή ο Ιάκωβος ο Πρωτοψάλτης; Τρελά πράγματα αγαπητέ Laviq27. Πότε θα μπορέσουμε να καταλάβουμε ότι η μουσική είναι πέρα απ’ το ανθρώπινο, δεν έχει αρχή ούτε τέλος, είναι φτιαγμένη με Θεία υλικά, γι’ αυτό προορίζεται για την ψυχή κι όχι για το σώμα μας. «Αγωγό Ψυχής» την αποκαλούσαν οι Αρχαίοι πρόγονοί μας, ενώ σήμερα την έχουμε καταντήσει «Αγωγό Ευρώ», όλα για το χρήμα. Ολίγον άστοχη η παρατήρησή σου για την κότα και το αυγό, αλλά δεν πειράζει, αλλά θα συμφωνήσω με το βιβλίο του M.L. West, για τη μουσική στην Αρχαία Ελλάδα, είναι πράγματι το καλύτερο που έχω διαβάσει, χωρίς όμως να αποτελεί και πανάκεια. Η μουσική μπορεί να εκφραστεί με μαθηματικά, όσον αφορά τα διαστήματα, τη χρονική διάρκεια των φθόγγων, την έντασή τους, τη χροιά τους. Το συναίσθημα όμως με ποια μαθηματικά μπορεί να εκφραστεί; Ας μας πει ο αγαπητός rapsodos με ποια μαθηματικά θα περιγράψουμε ένα solo του Gary Moore, του Santana ή ακόμα ένα solo του αξέχαστου Μανώλη Χιώτη. Για να μην αναφερθώ σε άλλα ιερά τέρατα εκτελεστών (όπως ο Ιωάννης ο Γλυκύς, ο Κωνσταντίνος Πρίγγος ο Πρωτοψάλτης, ο Γιώργος Μπατζανός, ο Ταμπούρι Τσεμίλ Μπέη, ο Νικολάκης ο Λυράρης, ο Μουνίρ Μπασιρ, ο Νικολό Παγκανίνι κ.α. ) ή συνθετών (όπως ο Κάρλ Ορφ, ο Βάγκνερ, Μπετόβεν, Ιάκωβος ο Πρωτοψάλτης, Γεώργιος ο Κρης κ.α. ). Όλοι οι παραπάνω πρέπει να είχαν διδακτορικό στα μαθηματικά. Να μην ξεχάσουμε τέλος και τον αείμνηστο Θρασύβουλο Στανίτσα, που δεν τελείωσε καλά καλά ούτε το δημοτικό σχολείο. Η μουσική του παιδεία, οι απαράμιλλες συνθέσεις του και η εκτελεστική του δεινότητα, θα μείνουν αξέχαστες και ανεπανάληπτες στα χρονικά. Στανίτσας ήταν μόνο ένας και δεν ήξερε μαθηματικά ! Τέλος πάντων, ας μη γίνω περισσότερο κακός και να σταματήσω λέγοντας: «Παν δώρημα τέλειον άνωθεν εστί». Έτσι και η μουσική σαν τέλειο δώρημα που είναι, πηγάζει απ’ το Θεό (όπως το κάθε τι βεβαίως), ο οποίος είναι ο μόνος τέλειος και κατακτάται στον ύψιστο βαθμό της, μόνο με την χάρη του Αγίου Πνεύματος. Για όσους θέλουν και μπορούν να καταλάβουν, ας το πιστέψουν και ας προσπαθήσουν με περισσότερη αγάπη και ευλάβεια, για όσους δεν θέλουν, δεν μπορούν ή δεν τους αφήνει ο εγωισμός τους, θα κολυμπούν για πάντα μέχρι εκεί που πατώνουν. Καλό καλοκαίρι και όχι στα βαθειά ! |
| #15394 / 15.07.2008, 13:54 / Αναφορά Έμεινα άφωνη! Κοίτα τι κάνουν τα μαθηματικά και εμείς μαθαίνουμε μπούρδες! |
| #15405 / 16.07.2008, 13:52 Καταρχήν, οφείλω να συγχαρώ τον αρθρογράφο για τον κόπο της σύνταξης του κειμένου. Υπάρχουν δε, αρκετές ασάφειες, που είναι φυσικό σε θέματα που γυρίζουν γύρω από την τέχνη. Θέλω μόνο να επισημάνω μία εξώφθαλμη. Τα μαθηματικά και η μουσική δεν είναι επιστήμες. Τα μαθηματικά και η μουσικοΛΟΓΙΑ είναι επιστήμες. Όλες οι παραπάνω αναλύσεις αφορούν τη μουσικολογία, που αναπτύχθηκε -έστω και σε πρώιμη μορφή- δεκάδες ή και εκατοντάδες χιλιετίες μουσικών αναζητήσεων του ανθρώπου. Ο "συγκερασμός", που αναφέρθηκε παραπάνω, είναι γνωστός με τη σύγχρονη μορφή του. Εντούτοις, απόπειρες συγκερασμού αλλά και μαθηματικές αναλύσεις αναλύσεις αυτού έχουν αναπτυχθεί από την Αρχαία Ελλάδα (πχ. Πυθαγόρας). Επί της ουσίας, συγκερασμός (συν-κερασμός= η μείωση,ελάττωση των αντιθέσεων/διαφορών) είναι η απόπειρα μαθηματικοποίησης των μουσικών διαστημάτων, ώστε να επιτευχθεί ακουστική σύζευξη (τομή) μεταξύ των οργάνων και μουσικών δρόμων. Ακόμα και σήμερα διατηρούνται διάφορες μορφές συγκερασμού, με ποιο διαδεδομένη αυτή της κλασικής εποχής. Συμφωνώ με το σχολιασμό του yiannis yiannis σε πολλά σημεία. |
| #24809 / 03.07.2012, 18:34 / Αναφορά Διόρθωσε δύο λαθάκια: Όταν δίνεις παράδειγμα διαστήματος 5ης γράφεις Ντο-Λα, ενώ το ορθό είναι Ντο-Σολ. Αντίστοιχα το παράδειγμά σου για διάστημα 4ης από Ντο-Σολ διόρθωσέ το σε Ντο-Φα. Τώρα, αν μπορείς, σε παρακαλώ να με παραπέμψεις σε κάποια ιστοσελίδα ή ... αρχείο ήχου, όπου θα διαβάσω ή θα μπορέσω να ακούσω παραδείγματα για ευρωπαϊκή (δυτική) μουσική ΠΡΙΝ από τον συγκερασμό. Π.χ. Απορία: Το πιάνο (και οι πρόγονοί του) ήταν ποτέ κουδισμένο σε μη συγκερασμένο τρόπο; Τα μουσικά κομμάτια πριν από την καθιέρωση του συγκερασμού σήμερα αποδίδονται μόνο με τον νέο τρόπο ή υπάρχει προσπάθεια να παιχθούν "ασυγκέραστα"; Συγγνὠμη, αν είναι αφελείς οι απορίες μου. Πάντως, θα σου ήμουν ευγνώμων, αν ακούσω παιγμένο από μουσικούς της ευρωπαϊκής μουσικής ένα τέτοιο ασυγκέραστο δείγμα. Ενδιαφέρον μεγάλο θα είχε αν μπορούσαμε να ακούσουμε το ίδιο κομμάτι παιγμένο και με τους δύο τρόπους! |
| #24810 / 03.07.2012, 21:16 Ρίξτε μια ματιά στις 4 ενότητες του άρθρου: http://www.musicheaven.gr/html/modules.php?name=News&file=article&sid=3297 που είναι συμπληρωματικό του παρόντος με περισσότερα σχεδιαγράμματα και ειδικά στο Pythagoras Intonation και άκουσε την ειδική κιθάρα αλλά δες πληροφορίες και για το ο πιάνο Garritan Steinway και το Pianoteq που έχει δυνατότητες Pythagoras Intonation.
|



 Η ιστορία του «Dress you up» της Madonna
Η ιστορία του «Dress you up» της Madonna Συχνά λάθη καθηγητών φωνητικής
Συχνά λάθη καθηγητών φωνητικής G.A.S (Gear aquisition syndrome)
G.A.S (Gear aquisition syndrome) Τεχνική στο τραγούδι: Σύμμαχος ή εχθρός της έκφρασης;
Τεχνική στο τραγούδι: Σύμμαχος ή εχθρός της έκφρασης; Είμαι παράφωνος. Μπορώ να τραγουδήσω;
Είμαι παράφωνος. Μπορώ να τραγουδήσω; Πώς μπορώ να τραγουδήσω σωστά τις ψηλές νότες;
Πώς μπορώ να τραγουδήσω σωστά τις ψηλές νότες;





